Space Apps Challenge 2018

Here's an overview on how our machine learning algorithm works:

For object detection it’s using faster R-CNN architecture. In a nutshell the intuition behind using a CNN network comes because they are known to be useful in image pattern matching tasks (as ours). That network “learns” the specific features to detect such impacts. The deeper the network, the more sophisticated the network becomes. Since, impacts can be seen just as lines or circles, just a few of layers (2 or 3) will be sufficient for our detection. Furthermore, this approach is resilience to light conditions, since filters of edges and simple shapes should be generated the same for photos with different light conditions.

In addition to the fact that object is detected, a region layer of this object is proposed and continued to the semantic segmentation phase.

For semantic segmentation it uses fully convolution network (FCN) to perform pixel classification (for the region layer), using a binary mask. In a FCN, appending a fully connected layer enables the network to learn something using global information where the spatial arrangement of the input falls away and need not apply.

Thus, with this algorithm, we will be able to detect impacts, and also to make a segmentation of them. This enables us to provide the spider-bot much richer information before it is sent.

Here is the introduction video to our presentation. Hope you like it!

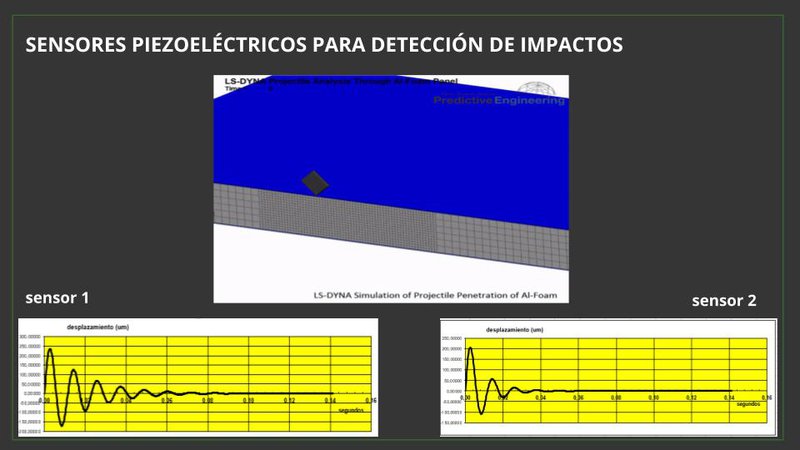
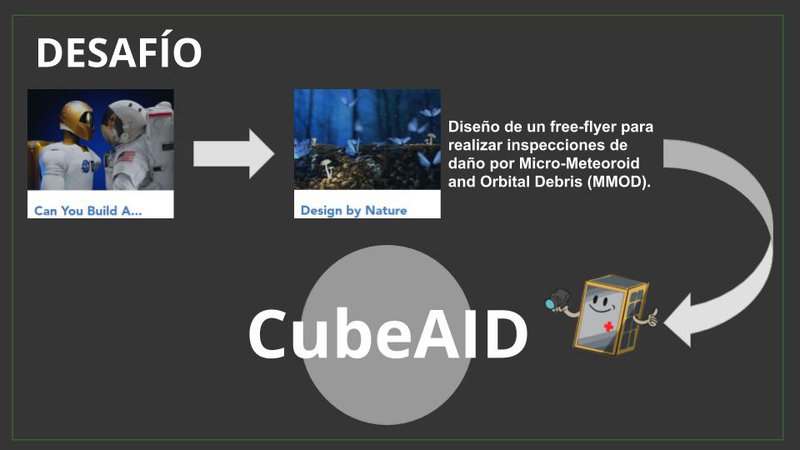
Space debree and micrometors post a threat to astronauts onboard the ISS and other spaceships. We can predict impacts, but not where they happen exactly on the outer surface of the ship. To that end, we developed CubeAID. A three phases system that detects, locates and repairs damage caused by microimpacts.

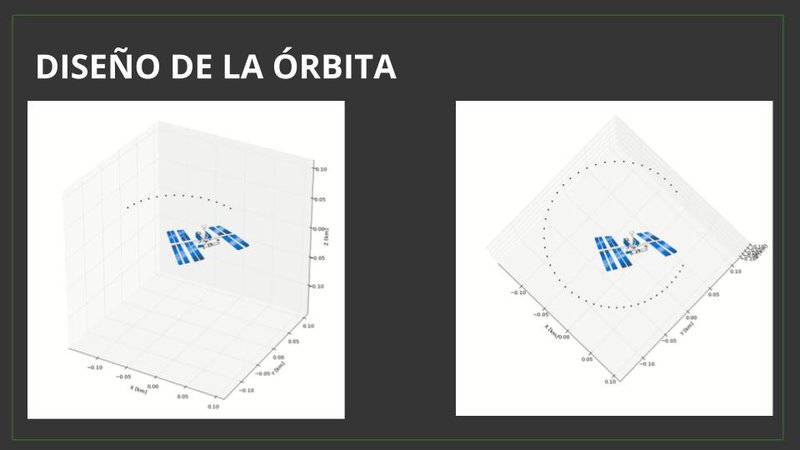
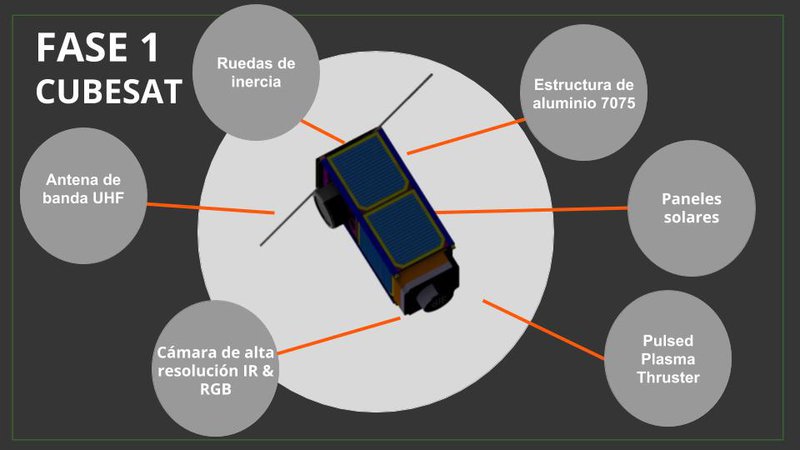
This is how it works. The cubesat orbit allows it to move around the ISS and cover all the possible angles. It takes pictures and sends it to the onboard computer of the ISS and using Watson Image Recognition it locates possible threats to the integrity of the ship.

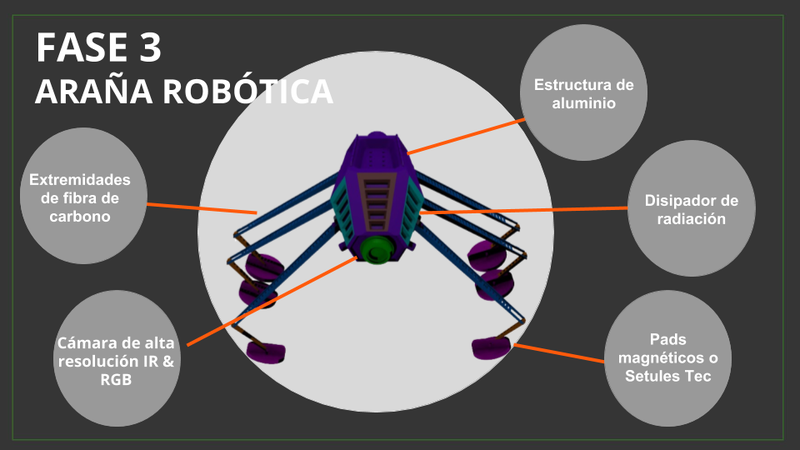
Once we know the location of the micrometeor impact, the spider robot comes out, analizes the surface and if needed repairs.

We have finished updating the project on the website, now we need to get to work on the video

We found out we won Best Use of Science and Best Mission Concept!! We are all so thrilled. Nonetheless the greatest happiness came because of working as a team in such an interesting project. I honestly did not expect to find such passionate and driven people, we all got together and communicated perfectly, there were absolutely no problems among us, we truly were a team. Thank you guys for the awesome experience!

Did you know?
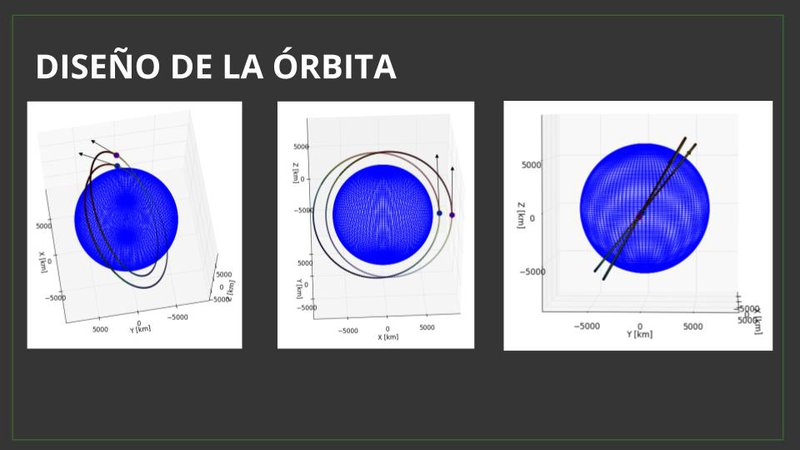
The ISS's orbit has a semiparameter of 6783km, the same as its semi major axis since its eccentricity is almost 0 (0.0004031 to be more precise). And it has an inclination of 51.6363 degrees.

Of course all of those values are changing constantly due to the many perturbations that exist in nature. Unfortunately there is no perfect conical orbit like Kepler predicted (but it is a great approximation if you are doing quick calculations).

This is how we shared our project with the jury and our fellow participants.

#Python code for orbit simulation (it is not completely finished, there are a few minor bugs and there are some functionalities that I still want to add)

#Sorry I didn't use github, for some reason I'm having trouble signing in

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as plt2

from mpl_toolkits.mplot3d import Axes3D

from matplotlib.patches import FancyArrowPatch

from mpl_toolkits.mplot3d import proj3d

import warnings

warnings.filterwarnings("ignore", message="numpy.dtype size changed")

from scipy.optimize import newton

#CONSTANTS---------------------------------------------

circ = 'Circular'

elli = 'Elliptical'

parab = 'Parabolic'

hyp = 'Hyperbolic'

equ = 'Equatorial'

inc = 'Inclined'

ecc = 'Eccentric'

mu_earth = 398600.4415 # [km^3/s^2]

mu_sun = 132712440018.9

eqR_earth = 6378.1363 # [km]

eqR_sun = 695700

itlim = 10000 # iteration limit

#FUNCTIONS---------------------------------------------

def getmu(): # Get mu (either load the defaults or get a custom one)

print ('\nInsert the Standard Gravitational Parameter (mu) - or insert \'E\' for Earth or \'S\' for the Sun')

mu = input()

if mu == 'E' or mu == 'e':

mu = mu_earth

elif mu == 'S' or mu == 's':

mu = mu_sun

else:

mu = abs(float(mu))

return mu

def ae2Eh(orb): # a, e -> E, h

if orb.a == 'Inf':

orb.E = 0 # Parabola, Energy=0

else:

orb.p = orb.a*(1-orb.e**2) # p = a(1-e^2)

orb.E = -orb.mu/(2*orb.a) # E = -mu/(2a)

orb.h = np.sqrt(orb.mu*orb.p) # h = sqrt(mu*p)

return

def Eh2ae(orb): # E, h -> a, e

if orb.E == 0:

orb.a = 'Inf' # Parabola, a=inf

orb.e = 1 # ^^, e=1 # p already loaded

else:

orb.a = -orb.mu/(2*orb.E) # a=-mu/(2E)

orb.p = orb.h**2/orb.mu # p=h^2/mu

aux = 2*orb.E*orb.h**2/orb.mu**2 # 2E*h^2/mu^2

if aux<-1:

orb.exist = 0 # Energy not permitted for given h

orb.e = -1 # To avoid comparison error later

else:

orb.e = np.sqrt(1+aux) # e=sqrt(1+2E*h^2/mu^2)

return

def Periap_Apoap(orb):

if orb.e != 1:

orb.rv_ap[0] = orb.a*(1-orb.e) # rp=a(1-e)

orb.rv_ap[2] = np.sqrt(orb.mu*(2/orb.rv_ap[0]-1/orb.a)) # vp=sqrt(mu(2/rp-1/a))

if orb.e<1:

orb.rv_ap[1] = orb.a*(1+orb.e) # ra=a(1+e)

orb.rv_ap[3] = np.sqrt(orb.mu*(2/orb.rv_ap[1]-1/orb.a)) # va=sqrt(mu(2/ra-1/a))

else:

orb.rv_ap[1] = 'Inf'

orb.rv_ap[3] = np.sqrt(2*orb.E) # vinf = sqrt(2E)

else:

orb.rv_ap[0] = orb.p/2 # rp=p/2

orb.rv_ap[1] = orb.a # ra=a

orb.rv_ap[2] = np.sqrt(2*orb.mu/rv_ap[0]) # vp=sqrt(2mu/rp)

orb.rv_ap[3] = 0 # Parabola, vinf=0

print ('Radius of Periapsis\t=\t', orb.rv_ap[0], '\tkm')

print ('Radius of Apoapsis\t=\t', orb.rv_ap[1], '\tkm')

print ('Periapsis Velocity\t=\t', orb.rv_ap[2], '\tkm/s')

print ('Apoapsis Velocity\t=\t', orb.rv_ap[3], '\tkm/s')

return

def graph2D(obj,save,name): # Graph the 2D orbit

plt.figure()

if obj.mu == mu_earth:

plt.gcf().gca().add_artist(plt.Circle((0,0),6378,color='b'))

else:

plt.gcf().gca().add_artist(plt.Circle((0,0),695700,color='y'))

if obj.e < 1: # Ellipse

plt.gcf().gca().add_artist(plt2.Ellipse((-obj.e*obj.a,0),2*obj.a,2*obj.a*np.sqrt(1-obj.e**2),fill=False)) # center at focal point (c=e*a), width=2*a, height=2*b=2*sqrt(1-e^2)

plt.xlim(-1.3*obj.a,1.3*obj.a)

plt.ylim(-1.3*obj.a*np.sqrt(1-obj.e**2),1.3*obj.a*np.sqrt(1-obj.e**2))

else:

nu = 0

X = np.array([rp,0])

r = 0

r_max = 10*rp

while r < r_max: # parabola or hyperbola, r limit, open orbit

r = obj.p/(1+obj.e*np.cos(nu)) # r=p/(1+e*cos(nu))

X = np.vstack([X,[r*np.cos(nu),r*np.sin(nu)]]) # x=rcos(nu), y=rsin(nu)

X = np.vstack([X,[r*np.cos(nu),-r*np.sin(nu)]]) # symmetry on Y

nu += 0.2*np.pi/180

plt.plot(X[:,0],X[:,1],'bo',markersize=1)

plt.axes().set_aspect('equal')

plt.xlabel('x [km]')

plt.ylabel('y [km]')

if save:

plt.savefig(name+'.png', bbox_inches='tight', dpi=300)

plt.show()

print (name+'.png successfully saved')

else:

plt.show()

return

def deg(rad): # radians to degrees

return rad*180/np.pi

def rad(deg): # degrees to radians

return deg*np.pi/180

def parAnom(x,B): # parabolic anomaly, M = B^3/3 + B

return x**3/3+x-B

def parAnomD1(x,B): # first derivative of ^^ (for better convergence to the zero)

return x**2+1

def parAnomD2(x,B): # second dervative ^^^

return 2*x

def MKepEqtnEBH(sat, abstol): # M -> E/B/H (im missing the parabolic case)

if sat.coe.e != 1: # circ, ellip or hyp

if sat.coe.e < 1: # starting point for iteration

anomp = sat.M - sat.coe.e

if sat.M < np.pi:

anomp += 2*sat.coe.e

else:

anomp = sat.M

anom = anomp + 2*abstol # so that it goes into the while loop at least once

c = 0 # iteration count

while abs(anom-anomp) > abstol and c < itlim:

anomp = anom

c += 1

if sat.coe.e < 1:

anom = anomp + (sat.M -anomp +sat.coe.e *np.sin(anomp)) /(1 -sat.coe.e *np.cos(anomp)) # anom[i] = anom[i-1]+(M-anom[i-1]+e*sin(anom[i-1]))/(1-e*cos(anom[i-1]))

else:

anom = anomp + (sat.M +anomp -sat.coe.e *np.sinh(anomp)) /(sat.coe.e *np.cosh(anomp)-1) # anom[i] = anom[i-1]+(M+anom[i-1]-e*sinh(anom[i-1]))/(e*cosh(anom[i-1])-1)

if c == itlim:

print ('\n\nCalulation stopped, iteration limit reached')

else: # parab

anom = newton(parAnom, 0, args=(sat.M,), fprime=parAnomD1, tol=abstol, maxiter=itlim, fprime2=parAnomD2) # Halley's method to find the zero (second derivative given, cubed convergence)

sat.anom = anom

return

def KepEqtnnu(sat): # E/H/B -> nu

if sat.coe.e < 1:

denom = 1 - sat.coe.e * np.cos(sat.anom) # aux = 1-e*cos(anom)

sat.coe.nu = np.arctan2((np.sin(sat.anom)*np.sqrt(1-sat.coe.e**2))/denom , (np.cos(sat.anom)-sat.coe.e)/denom) # sin(nu)=sin(E)*sqrt(1-e^2)/aux cos(nu)=(cos(E)-e)/aux

elif sat.coe.e == 1:

sat.coe.nu = 2*np.arctan(sat.anom) # nu=2*arctan(B)

else:

denom = 1 - sat.coe.e * np.cosh(sat.anom) # aux=1-e*cosh(H)

sat.coe.nu = np.arctan2((-np.sinh(sat.anom)*np.sqrt(sat.coe.e**2-1))/denom , (np.cosh(sat.anom)-sat.coe.e)/denom) # sin(nu)=-sinh(H)*sqrt(e^2-1)/aux cos(nu)=(cosh(H)-e)/aux

return

def KepEqtnM(sat): # E/H/B -> M

if sat.coe.e < 1:

sat.M = sat.anom - sat.coe.e * np.sin(sat.anom) # M=E-e*sin(E)

elif sat.coe.e == 1:

sat.M = sat.anom + sat.anom**3/3 # M=B+B^3/3

else:

sat.M = sat.coe.e * np.sinh(sat.anom) - sat.anom # M=e*sinh(H)-H

return

def nuKepEqtnEBH(sat): # nu -> E/B/H

if sat.coe.e == 1:

sat.anom = np.tan(sat.coe.nu/2) # B=tan(nu/2)

elif sat.coe.e < 1:

if sat.coe.e < 1:

arg = 1-sat.coe.e**2 # aux1E=1-e^2

else:

arg = sat.coe.e**2-1 # aux1H=e^2-1

denom = 1+sat.coe.e*np.cos(sat.coe.nu) #aux2=1+e*cos(nu)

sat.anom = np.arctan2((np.sin(sat.coe.nu)*np.sqrt(arg))/denom , (sat.coe.e+np.cos(sat.coe.nu))/denom) # sin(anom)=sin(nu)*sqrt(aux1)/aux2 cos(anom)=(e+cos(nu))/aux2

else:

term = np.sqrt((sat.coe.e-1.)/(sat.coe.e+1.)) * np.tan(0.5*sat.coe.nu) # aux = tan(nu/2)*sqrt((e-1)/(e+1))

sat.anom = 2.*np.arctanh(term)

return

def plotfile(array, markx, marky, x, y, xl, yl, save): # plot anomalies

plt.figure()

plt.plot(array[:,x],array[:,y],'bo',markersize=0.2) # data from file

plt.gcf().gca().add_artist(plt.Circle((markx,marky),3,color='r')) # user's entry

plt.axes().set_aspect('equal')

plt.xlabel(xl)

plt.ylabel(yl)

plt.ylim(-180,180)

plt.grid(b=True, which='both', axis='both')

if save:

print ('Insert file name (will be saved as png)')

name = input()

plt.title(name)

plt.savefig(name+'.png', bbox_inches='tight', dpi=300)

print (name+'.png successfully saved')

else:

plt.show()

return

def get_e_a(orb): # get the semi major axis and eccentricity

print ('Insert Major Semi-axis [km] (value will be turned negative for hyperbolas, if a=inf input inf)')

orb.a = input()

while orb.a == '0':

print ('Linear orbits not accepted, insert again')

orb.a = input()

if orb.a == 'inf' or orb.a == 'Inf':

orb.a = 'Inf'

print ('Eccentricity = 1, insert Periapsis Radius [km]')

orb.e = 1

orb.p = 2*abs(float(input()))

else:

orb.a = abs(float(orb.a))

print ('Insert Eccentricity')

orb.e = float(input())

while orb.e < 0 or orb.e == 1:

print ('Eccentricity value must be positive and not 1 (because a is not inf), insert again')

orb.e = float(input())

if orb.e > 1:

orb.a = -orb.a

orb.p = orb.a * (1-orb.e**2) # p=a(1-e)

return

def getnu_lim(sat): # get a valid value of nu (limited for hyperbolas)

i = 0 #loop counter

print ('Insert True Anomaly [deg]')

if sat.coe.e <= 1:

sat.coe.nu = rad(float(input()))

while sat.coe.nu >= 2*np.pi: # so that the angle is between 0 and 2pi

sat.coe.nu -= 2*np.pi

i += 1

while sat.coe.nu < 0:

sat.coe.nu += 2*np.pi

i -= 1

else:

sat.coe.nu = 10 # so that it goes into the while loop

limit = np.pi-np.arccos(1/sat.coe.e)

while sat.coe.nu >= limit or sat.coe.nu <= -limit: # nu limit given e

if sat.coe.nu != 10:

print ('Value not possible for given e, insert again')

sat.coe.nu = rad(float(input()))

while sat.coe.nu > np.pi: # so that the angle is between -pi and pi

sat.coe.nu -= 2*np.pi

while sat.coe.nu <= -np.pi:

sat.coe.nu += 2*np.pi

return i

def getTOF(sat1, sat2): # get time of flight

if sat1.orb.e != 1:

n = np.sqrt(sat1.orb.mu/(abs(sat1.orb.a)**3)) # mean motion, sqrt(mu/a^3)

if sat1.orb.e < 1:

tof = ((sat2.anom-sat2.orb.e*np.sin(sat2.anom)) - (sat1.anom-sat2.orb.e*np.sin(sat1.anom))) /n # tof=((E2-e*sin(E2)-(E1-e*sin(E1))/n

else:

tof = ((sat2.coe.e*np.sinh(sat2.anom)-sat2.anom) - (sat1.coe.e*np.sinh(sat1.anom)-sat1.anom)) /n # tof=((e*sinh(H2)-H2)-(e*sinh(H1)-H1))/n

else:

n = 2*np.sqrt(sat1.orb.mu/sat1.orb.p**3) # mean motion, 2*sqrt(mu/p^3)

tof = ((sat2.anom**3/3+sat2.anom) - (sat1.anom**3/3+sat1.anom)) /n # tof=((B2^3/3+B2)-(B1^3/3+B1))/n

return tof

def TOF2nu(sat1,sat2,tof): # calculate nu2 from TOF

if sat1.orb.e != 1:

n = np.sqrt(sat1.orb.mu/(abs(sat1.orb.a)**3)) # mean motion, sqrt(mu/a^3)

else:

n = 2*np.sqrt(sat1.orb.mu/sat1.orb.p**3) # 2*sqrt(mu/p^3)

sat1.compKep(1e-6)

sat2.M = tof * n + sat1.M # Mf=tof*n+Mi

sat2.compKep(1e-6)

return

def RV2COE(sat): # rv -> COE

print('r',sat.r)

print('v',sat.v)

sat.orb.hv = np.cross(sat.r,sat.v) # hv=rxv

print('h',sat.orb.hv, np.sqrt(np.dot(sat.orb.hv,sat.orb.hv)))

n = np.cross(np.array([0,0,1]),sat.orb.hv) # line of nodes=kxhv

print('n',n)

vm2 = np.dot(sat.v,sat.v)

print('vm', np.sqrt(vm2))

rm2 = np.dot(sat.r,sat.r)

rm = np.sqrt(rm2)

print('rm',rm)

sat.orb.ev = ((vm2-sat.orb.mu/rm)*sat.r-(np.dot(sat.r,sat.v))*sat.v)/sat.orb.mu # ev=((vm2-mu/rm)*r-(r.v)*v)/mu

print('ev',sat.orb.ev)

sat.orb.E = vm2/2-sat.orb.mu/rm # E=vm2/2-mu/rm

print('E',sat.orb.E)

em2 = np.dot(sat.orb.ev,sat.orb.ev)

sat.coe.e = np.sqrt(em2)

print('e',sat.coe.e)

if em2 != 1: # not parab

sat.coe.a = sat.orb.a = -sat.orb.mu/(2*sat.orb.E) # a=-mu/2E

sat.coe.p = sat.orb.p = sat.orb.a*(1-em2) # p=a*(1-em2)

else: # parab

sat.coe.p = sat.orb.p = np.dot(sat.orb.hv,sat.orb.hv)/sat.orb.mu # p=hm2/mu

sat.coe.a = sat.orb.a = 'Inf'

sat.coe.i = np.arccos(sat.orb.hv[2]/np.sqrt(np.dot(sat.orb.hv,sat.orb.hv))) # i=arccos(h(z)/hm)

nm2 = np.dot(n,n)

if nm2 != 0 and em2 != 0: # ellip inclined

sat.coe.RAAN = np.arccos(n[0]/np.sqrt(nm2)) # raan=arccos(n(x)/nm)

if n[1]<0:

sat.coe.RAAN = 2*np.pi - sat.coe.RAAN

while sat.coe.RAAN > np.pi:

sat.coe.RAAN -= 2*np.pi

sat.coe.w = np.arccos(np.dot(n,sat.orb.ev)/np.sqrt(nm2*em2)) # w=arccos(n.e/(nm*em))

if sat.orb.ev[2]<0:

sat.coe.w = 2*np.pi - sat.coe.w

while sat.coe.w > np.pi:

sat.coe.w -= 2*np.pi

sat.coe.nu = np.arccos(np.dot(sat.r,sat.orb.ev)/(rm*sat.coe.e)) # nu=arccos(r.e/(rm*em))

if np.dot(sat.r,sat.v)<0:

sat.coe.nu = 2*np.pi - sat.coe.nu

while sat.coe.nu > np.pi:

sat.coe.nu -= 2*np.pi

sat.coe.wtr = sat.coe.u = sat.coe.trlong = 'Not calculated'

else:

sat.coe.RAAN = sat.coe.w = sat.coe.nu = 'Undef'

if em2 != 0: #ellip equatorial

sat.coe.wtr = np.arccos(sat.orb.ev[0]/np.sqrt(em2)) # wtr=arccos(e(x)/em)

if sat.orb.ev[1]<0:

sat.coe.wtr = 2*np.pi - sat.coe.wtr

while sat.coe.wtr > np.pi:

sat.coe.wtr -= 2*np.pi

sat.coe.u = sat.coe.trlong = 'Not calculated'

sat.coe.nu = np.arccos(np.dot(sat.r,sat.orb.ev)/(rm*sat.coe.e)) # nu=arccos(r.e/(rm*em))

if np.dot(sat.r,sat.v)<0:

sat.coe.nu = 2*np.pi - sat.coe.nu

while sat.coe.nu > np.pi:

sat.coe.nu -= 2*np.pi

elif nm2 != 0: #circ inclined

sat.coe.RAAN = np.arccos(n[0]/np.sqrt(nm2)) # raan=arccos(n(x)/nm)

if n[1]<0:

sat.coe.RAAN = 2*np.pi - sat.coe.RAAN

while sat.coe.RAAN > np.pi:

sat.coe.RAAN -= 2*np.pi

sat.coe.u = np.arccos(np.dot(n,sat.r)/np.sqrt(nm2*rm2)) # u=arccos(n.r/(nm*rm))

if sat.r[2]<0:

sat.coe.u = 2*np.pi - sat.coe.u

while sat.coe.u > np.pi:

sat.coe.u -= 2*np.pi

sat.coe.wtr = sat.coe.trlong = 'Not calculated'

else: #circ equatorial

sat.coe.trlong = np.arccos(r[0]/rm) # trlong=arccos(r(x)/rm)

if sat.r[1] < 0:

sat.coe.trlong = 2*np.pi - sat.coe.trlong

while sat.coe.trlong > np.pi:

sat.coe.trlong -= 2*np.pi

sat.coe.wtr = sat.coe.u = 'Not calculated'

return

def COE2RV(sat):

if not (type(sat.coe.trlong) is str): # circ eq

sat.coe.w = sat.coe.RAAN = 0

sat.coe.nu = sat.coe.trlong

if not (type(sat.coe.u) is str): # circ inc

sat.coe.w = 0

sat.coe.nu = sat.coe.u

if not (type(sat.coe.wtr) is str): # ellip eq

sat.coe.RAAN = 0

sat.coe.w = sat.coe.wtr

cosnu = np.cos(sat.coe.nu)

sinnu = np.sin(sat.coe.nu)

rpqw = np.array([sat.coe.p*cosnu/(1+sat.coe.e*cosnu), sat.coe.p*sinnu/(1+sat.coe.e*cosnu), 0])

vpqw = np.array([-np.sqrt(sat.orb.mu/sat.coe.p)*sinnu, np.sqrt(sat.orb.mu/sat.coe.p)*(sat.coe.e+cosnu), 0])

cosraan = np.cos(sat.coe.RAAN)

sinraan = np.sin(sat.coe.RAAN)

cosw = np.cos(sat.coe.w)

sinw = np.sin(sat.coe.w)

cosi = np.cos(sat.coe.i)

sini = np.sin(sat.coe.i)

MAT = np.array([[cosraan*cosw-sinraan*sinw*cosi, -cosraan*sinw-sinraan*cosw*cosi, sinraan*sini],[sinraan*cosw+cosraan*sinw*cosi, -sinraan*sinw+cosraan*cosw*cosi, -cosraan*sini],[sinw*sini, cosw*sini, cosi]])

sat.r = np.dot(MAT,rpqw)

sat.v = np.dot(MAT,vpqw)

return

def propagate(sat):

print ('Insert initial and final times [s]') #is it in seconds??

t0 = float(input())

tf = float(input())

print ('Insert time step')

step = float(input())

t = np.arange(t0,tf,step) # time vector

N = len(t)

satsim = Satellite()

satsim = sat

X = np.zeros([N,7])

X[:,0] = np.concatenate([t]) # first column is time

X[0,1:] = np.concatenate([satsim.r, satsim.v]) # 1 to 3 r and 4 to 6 v

if sat.coe.e != 1:

n = np.sqrt(sat.orb.mu/(abs(sat.orb.a)**3)) # mean motion

else:

n = 2*np.sqrt(sat.orb.mu/sat.orb.p**3) # ^

for i in range(1,N): # for all time

if satsim.coe.e != 0:

satsim.compKep(1e-6)

#anom0 = satsim.anom

else:

if type(satsim.coe.u) == str:

anom0 = satsim.coe.trlong

else:

anom0 = satsim.coe.u

#print('anom0',anom0)

if satsim.coe.e != 1:

#M0 = anom0 - satsim.coe.e*np.sin(anom0)

#print (M0==satsim.M)

#satsim.M = M0 + n*step

satsim.M += n*step

else:

fds=0#COMPLETE

#print('M0',M0)

#print('M',satsim.M)

#print('anom',satsim.anom)

satsim.compKep(1e-6)

#print('M',satsim.M)

#print('anom',satsim.anom)

if satsim.coe.e == 0:

if satsim.coe.i == 0 or satsim.coe.i == np.pi:

satsim.coe.trlong = satsim.anom

satsim.coe.nu = satsim.coe.u = '...'

else:

satsim.coe.u = satsim.anom

satsim.coe.nu = satsim.coe.trlong = '...'

#print('nu',satsim.coe.nu)

satsim.sRV()

X[i,1:] = np.concatenate([satsim.r, satsim.v])

return X

def graph3D(sat):

fig = plt.figure()

ax = fig.gca(projection='3d')

ax.set_aspect('equal')

if sat.orb.mu == mu_earth:

R = eqR_earth

col = 'b'

else:

R = eqR_sun

col = 'y'

u, v = np.mgrid[0:2*np.pi:100j, 0:np.pi:100j]

x = R*np.cos(u)*np.sin(v)

y = R*np.sin(u)*np.sin(v)

z = R*np.cos(v)

ax.plot_wireframe(x, y, z, color=col)

ax.scatter(sat.r[0], sat.r[1], sat.r[2], color='r', s=100) # sat

a = Arrow3D([sat.r[0],sat.r[0]+1000*sat.v[0]], [sat.r[1],sat.r[1]+1000*sat.v[1]], [sat.r[2],sat.r[2]+1000*sat.v[2]], mutation_scale=20,lw=1, arrowstyle="-|>", color="k") # v vector

ax.add_artist(a)

X = propagate(sat)

ax.scatter(X[:,1],X[:,2],X[:,3],c=(X[:,1]+X[:,2]+X[:,3]),s=10)

ax.set_xlabel('X [km]')

ax.set_ylabel('Y [km]')

ax.set_zlabel('Z [km]')

minval=np.array([np.amin(x),np.amin(y),np.amin(z),np.amin(X[:,1]),np.amin(X[:,2]),np.amin(X[:,3])])

maxval=np.array([np.amax(x),np.amax(y),np.amax(z),np.amax(X[:,1]),np.amax(X[:,2]),np.amax(X[:,3])])

totmin = np.amin(minval)

totmax = np.amax(maxval)

ax.set_xlim3d(totmin, totmax)

ax.set_ylim3d(totmin, totmax)

ax.set_zlim3d(totmin, totmax)

plt.show()

return

#CLASSES---------------------------------------------

class Orbit: # Object that contains all orbit parameters

otype = '...' # Type of orbit (Circular, Elliptical, Parabolic, Hyperbolic)

itype = '...' # Type of orbit (Equatorial, Inclined)

mu = '...' # Standard Gravitational Parameter [km^3/s^2]

a = '...' # Major Semi-Axis [km]

e = '...' # Eccentricity [_]

ev = np.array([0.0,0.0,0.0]) # Eccentricity vector [_]

E = '...' # Specific Energy [km^2/s^2]

h = '...' # Specific Angular Momentum [km^2/s]

hv = np.array([0.0,0.0,0.0]) # ^^^ vector [km^2/s]

p = '...' # Semiparameter [km]

exist = 1 # If the orbit exists (E and h logical values) 1, else 0

rv_ap = np.array([0.0,0.0,0.0,0.0]) # Radius of periapsis, of apoapsis, velocity at per and apo

def loadmu(self): # Get the value of mu

self.mu = getmu()

def assign(self):

if self.e == 1:

self.otype = parab

elif self.e == 0:

self.otype = circ

elif self.e < 1:

self.otype = elli

else:

self.otype = hyp

def complete(self): # Calculate remainding values

if self.a != '...':

ae2Eh(self)

else:

Eh2ae(self)

self.assign()

def per_apo(self): # Calculate periapsis and apoapsis radii and velocities

Periap_Apoap(self)

def plot(self): # Graph the orbit

graph2D(self,False,0)

print ('Do you wish to save the graph? (Y/N)')

save = input()

if save=='Y' or save=='y':

print ('Insert file name (will be saved as png)')

name = input()

graph2D(self,True,name)

def printval(self): # Print the values

print ('Type of orbit\t\t=\t', self.otype)

print ('Major Semi-axis\t\t=\t', self.a, '\tkm')

print ('Eccentricity\t\t=\t', self.e)

print ('Specific Energy\t\t=\t', self.E, '\tkm^2/s^2')

print ('Angular Momentum\t=\t', self.h, '\tkm^2/s')

print ('Semi-parameter\t\t=\t', self.p, '\tkm\n\n')

class COE: # Classical Orbital Elements

p = '...' # Semiparameter [km]

a = '...' # Major Semi-Axis [km]

e = '...' # Eccentricity [_]

i = '...' # Inclination [rad]

RAAN = '...' # Right Ascension of the Ascending Node [rad]

w = '...' # Argument of Perigee [rad]

nu = '...' # True Anomaly [rad]

wtr = '...' # True Longitude of Periapsis [rad]

u = '...' # Argument of Latitude [rad]

trlong = '...' # True Longitude [rad]

class Satellite: # Object for a satellite in orbit

r = np.array([0.0,0.0,0.0]) # Position vector at time t [km]

v = np.array([0.0,0.0,0.0]) # Velocity vector at time t [km/s]

t = 0 # Point in ime [...]

anom = '...' # E/H/B anomaly

M = '...' # Mean anomaly

anomtype = '...' # Eccentric/Parabolic/Hyperbolic

def __init__(self):

self.orb = Orbit() # Orbit in which the satellite is contained

self.coe = COE() # COE

def compKep(self, abstol): # Complete the values from Kepler equation (nu, M anom)

if self.M != '...':

MKepEqtnEBH(self,abstol)

KepEqtnnu(self)

elif self.anom != '...':

KepEqtnM(self)

KepEqtnnu(self)

else:

nuKepEqtnEBH(self)

KepEqtnM(self)

if self.coe.e < 1:

self.anomtype = ecc

elif self.coe.e == 1:

self.anomtype = parab

else:

self.anomtype = hyp

def sCOE(self): # Get COE from r and v

RV2COE(self)

def sRV(self): # Get r and v from COE

COE2RV(self)

def plot(self): # Graph the orbit with the satellite

graph3D(self)

class Arrow3D(FancyArrowPatch):

def __init__(self, xs, ys, zs, *args, **kwargs):

FancyArrowPatch.__init__(self, (0, 0), (0, 0), *args, **kwargs)

self._verts3d = xs, ys, zs

def draw(self, renderer):

xs3d, ys3d, zs3d = self._verts3d

xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)

self.set_positions((xs[0], ys[0]), (xs[1], ys[1]))

FancyArrowPatch.draw(self, renderer)

#MAIN PROGRAM---------------------------------------------

print ('\n\n-------------------------------ASTRODYNAMICS--------------------------------')

print ('Developed by: Tomas Burroni\n\n')

opt = 0

while opt != 'q': # Program MENU

print ('Select an option or press \'q\' to exit the program')

print ('2D Orbits:')

print ('\t1) Calculate Specific Energy and Angular Momentum from Major Semi-axis and Eccentricity')

print ('\t2) Calculate Major Semi-axis and Eccentricity from Specific Energy and Angular Momentum')

print ('Kepler Equation:')

print ('\t3) Calculate Anomalies from Mean Anomaly and Eccentricity')

print ('\t4) Calculate Anomalies from True Anomaly and Eccentricity')

print ('\t5) Calculate Anomalies from Eccentric/Parabolic/Hyperbolic Anomaly and Eccentricity')

print ('\t6) Calculate Time of Flight')

print ('\t7) Calculate final True Anomaly from TOF')

print ('Classical Orbital Elements')

print ('\t8) Calculate Orbital Elements from position and velocity')

print ('\t9) Calculate position and velocity from Orbital Elements')

opt = input()

if opt == 'q' or opt == 'Q':

break

else:

opt = int(opt)

if opt < 0 or opt > 10:

print ('Invalid option, select again')

else:

if opt == 1: # Option 1 - a,e -> E,h

orb = Orbit()

orb.loadmu()

get_e_a(orb)

orb.complete()

print ('\n--------------------Results--------------------')

orb.printval()

print ('Do you want aditional parameters (r and v at periapsis and apoapsis)? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

orb.per_apo()

print ('Do you wish to plot the orbit? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

orb.plot()

elif opt == 2: # Option 2 - E,h -> a,e

orb = Orbit()

orb.loadmu()

print ('Insert Specific Energy [km^2/s^2]')

orb.E = float(input())

if orb.E == 0:

print ('Another parameter will be needed\nInsert Periapsis Radius [km]')

orb.p = 2*abs(float(input()))

while orb.p == 0:

print ('Linear orbits not supported, insert again')

orb.p = 2*abs(float(input()))

print ('Insert Angular Momentum [km^2/s]')

orb.h = abs(float(input()))

orb.complete()

if orb.exist:

print ('\n--------------------Results--------------------')

orb.printval()

print ('Do you want aditional parameters (r and v at periapsis and apoapsis)? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

orb.per_apo()

print ('Do you wish to plot the orbit? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

orb.plot()

else:

print ('\nE and h values do not make an orbit\n\n')

elif opt == 3: # Option 3 - M -> E/B/H, nu

sat = Satellite()

print ('Insert eccentricity')

sat.coe.e = float(input())

while sat.coe.e < 0:

print ('Eccentricity must be positive, insert again')

sat.coe.e = float(input())

print ('Insert Mean anomaly [deg]')

sat.M = rad(float(input()))

if sat.coe.e < 1:

while sat.M > np.pi: # so that the angle is between -pi and pi

sat.M -= 2*np.pi

while sat.M <= -np.pi: # ^^

sat.M += 2*np.pi

print ('Insert maximum allowed error - or insert \'def\' or \'0\' for default value of 1e-6')

abstol = input()

if abstol == 'def' or abstol == '0':

abstol = 1e-6

else:

abstol = float(abstol)

sat.compKep(abstol)

print ('\n--------------------Results--------------------')

print ('True Anomaly\t\t=\t',deg(sat.coe.nu))

print (sat.anomtype,'Anomaly\t=\t',deg(sat.anom))

print ('Mean Anomaly\t\t=\t',deg(sat.M),'\n\n')

elif opt == 4: # Option 4 - nu -> E/H/B, M

sat = Satellite()

print ('Insert eccentricity')

sat.coe.e = float(input())

while sat.coe.e < 0:

print ('Eccentricity must be positive, insert again')

sat.coe.e = float(input())

getnu_lim(sat)

sat.compKep(0)

print ('\n--------------------Results--------------------')

print ('True Anomaly\t\t=\t',deg(sat.coe.nu))

print (sat.anomtype,'Anomaly\t=\t',deg(sat.anom))

print ('Mean Anomaly\t\t=\t',deg(sat.M),'\n\n')

elif opt == 5: # Option 5 - E/H/B -> M, nu

sat = Satellite()

print ('Insert eccentricity')

sat.coe.e = float(input())

while sat.coe.e < 0:

print ('Eccentricity must be positive, insert again')

e = float(input())

print ('Insert Anomaly [deg]')

if sat.coe.e > 1:

sat.coe.nu = 10 # so that it goes into the while loop

limit = np.pi-np.arccos(1/sat.coe.e)

while sat.coe.nu >= limit or sat.coe.nu <= -limit: # nu limit given e

if sat.coe.nu != 10:

print ('Value not possible for given e, insert again')

sat.anom = rad(float(input()))

while sat.anom > np.pi: # so that the angle is between -pi and pi

sat.anom -= 2*np.pi

while sat.anom <= -np.pi:

sat.coe.nu += 2*np.pi

KepEqtnnu(sat)

else:

sat.anom = rad(float(input()))

while sat.anom > np.pi: # so that the angle is between -pi and pi

sat.anom -= 2*np.pi

while sat.anom <= -np.pi:

sat.anom += 2*np.pi

sat.compKep(0)

print ('\n--------------------Results--------------------')

print ('True Anomaly\t\t=\t',deg(sat.coe.nu))

print (sat.anomtype,'Anomaly\t=\t',deg(sat.anom))

print ('Mean Anomaly\t\t=\t',deg(sat.M),'\n\n')

elif opt == 6: # Option 6 - TOF

sat1 = Satellite()

sat2 = Satellite()

sat1.orb.loadmu()

get_e_a(sat1.orb)

sat2.orb.e = sat2.coe.e = sat1.coe.e = sat1.orb.e # in order to get nu

i1 = getnu_lim(sat1)

i2 = getnu_lim(sat2)

nuKepEqtnEBH(sat1)

nuKepEqtnEBH(sat2)

if sat1.orb.e < 1: # if closed orbit, actual number of turns

sat1.anom += 2 * np.pi * i1

sat2.anom += 2 * np.pi * i2

tof = getTOF(sat1, sat2)

print ('\n--------------------Results--------------------')

print ('\nTOF\t=\t', tof, 's\t=\t', tof/3600, 'hs\n\n')

elif opt == 7: # Option 7 - TOF,nu1 -> nu2

sat1 = Satellite()

sat2 = Satellite()

sat1.orb.loadmu()

get_e_a(sat1.orb)

sat2.orb.e = sat2.coe.e = sat1.coe.e = sat1.orb.e

getnu_lim(sat1)

print ('Insert Time of Flight [s]')

tof = float(input())

TOF2nu(sat1,sat2,tof)

print ('\n--------------------Results--------------------')

print ('TOF\t=\t',tof,'\ts')

print ('nu0\t=\t',deg(sat1.coe.nu),'\tdeg')

print ('nu1\t=\t',deg(sat2.coe.nu),'\tdeg\n\n') # para graficar ver pagina 116(pdf) del vallado, ahi dice x, vx, y, vy en funcion de e y E/B/H

elif opt == 8: # Option 8 - r,v -> COE

sat = Satellite()

sat.orb.loadmu()

print ('Insert the three components for position [X,Y,Z] [km]')

for i in range(0,3):

sat.r[i] = float(input())

print ('Insert the three components for velocity [X,Y,Z] [km/s]')

for i in range(0,3):

sat.v[i] = float(input())

sat.sCOE()

print ('\n--------------------Results--------------------')

print ('Semiparameter\t\t\t=\t',sat.coe.p,'km')

print ('Major Semi-Axis\t\t\t=\t',sat.coe.a,'km')

print ('Eccentricity\t\t\t=\t',sat.coe.e)

print ('Inlination\t\t\t=\t',deg(sat.coe.i),'deg')

if type(sat.coe.RAAN) is str:

print ('RAAN\t\t\t\t=\t Undefined')

else:

print ('RAAN\t\t\t\t=\t',deg(sat.coe.RAAN),'deg')

if type(sat.coe.w) is str:

print ('Argument of Perigee\t\t=\t Undefined')

else:

print ('Argument of Perigee\t\t=\t',deg(sat.coe.w),'deg')

if type(sat.coe.nu) is str:

print ('True Anomaly\t\t\t=\t Undefined')

else:

print ('True Anomaly\t\t\t=\t',deg(sat.coe.nu),'deg')

if type(sat.coe.wtr) is str:

print ('True Longitude of Periapsis\t=\t Not calculated')

else:

print ('True Longitude of Periapsis\t=\t',deg(sat.coe.wtr),'deg')

if type(sat.coe.u) is str:

print ('Argument of Latitude\t\t=\t Not calculated')

else:

print ('Argument of Latitude\t\t=\t',deg(sat.coe.u),'deg')

if type(sat.coe.trlong) is str:

print ('True Longitude\t\t\t=\t Not calculated\n\n\n')

else:

print ('True Longitude\t\t\t=\t',deg(sat.coe.trlong),'deg\n\n\n')

print ('Do you want the 3D plot? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

sat.plot()

elif opt == 9: # Option 9 - COE -> r,v

sat = Satellite()

sat.orb.loadmu()

get_e_a(sat.orb)

sat.coe.a = sat.orb.a

sat.coe.e = sat.orb.e

sat.coe.p = sat.orb.p

print ('Inlination [deg]')

sat.coe.i = rad(float(input()))

if sat.coe.e == 0 or sat.coe.i == 0 or sat.coe.i == np.pi: # not ellip incl

sat.coe.w = 'Und'

print ('Argument of Perigee is Undefined')

if sat.coe.e != 0: # ellip equat

print ('RAAN is not defined')

print ('True Longitude of Periapsis [deg]')

sat.coe.wtr = rad(float(input()))

sat.coe.RAAN = 'Und'

sat.coe.u = sat.coe.trlong = 'NC'

elif sat.coe.i != 0 and sat.coe.i != np.pi: # circ incl

print ('RAAN [deg]')

sat.coe.RAAN = rad(float(input()))

print ('Argument of Latitude [deg]')

sat.coe.u = rad(float(input()))

sat.coe.wtr = sat.coe.trlong = 'NC'

else: # circ equat

print ('RAAN is not defined')

print ('True Lognitude [deg]')

sat.coe.trlong = rad(float(input()))

sat.coe.RAAN = 'Und'

sat.coe.wtr = sat.coe.u = 'NC'

else:

print ('RAAN [deg]')

sat.coe.RAAN = rad(float(input()))

print ('Argument of Perigee [deg]')

sat.coe.w = rad(float(input()))

sat.coe.wtr = sat.coe.u = sat.coe.trlong = 'NC'

if sat.coe.e == 0:

sat.coe.nu = 'Und'

print ('True Anomaly is not Defined')

else:

print ('True Anomaly [deg]')

sat.coe.nu = rad(float(input()))

sat.sRV()

print ('\n--------------------Results--------------------')

print ('Position [km]')

print(sat.r)

print ('Velocity [km/s]\n')

print(sat.v,'\n\n\n')

print ('Do you want the 3D plot? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

sat.plot()

if opt > 2 and opt < 6: # graph anomalies

print ('Do you want to plot the anomalies? (Y/N)')

ans = input()

if ans == 'Y' or ans == 'y':

if sat.coe.e < 1:

filename = 'Ellip-nu_E_M.dat'

var = 'E'

elif sat.coe.e > 1:

filename = 'Hyperb-nu_H_M.dat'

var = 'H'

else:

filename = 'Parab-nu_B_M.dat'

var = 'B'

Mvnu_Anom = np.loadtxt(filename,delimiter=',') # load a matrix with the data in the file for the plot

Mvnu_Anom = deg(Mvnu_Anom)

if sat.coe.nu > np.pi: # center everything between -pi and pi

sat.coe.nu -= 2*np.pi

if sat.anom > np.pi:

sat.anom -= 2*np.pi

if sat.M > np.pi:

sat.M -= 2*np.pi

plotfile(Mvnu_Anom, deg(sat.coe.nu), deg(sat.M), 0, 2, 'nu [deg]','M [deg]',False)

print ('Do you wish to save the graph? (Y/N)')

save = input()

if save == 'Y' or save == 'y':

plotfile(Mvnu_Anom, deg(sat.coe.nu), deg(sat.M), 0, 2, 'nu [deg]','M [deg]',True)

plotfile(Mvnu_Anom, deg(sat.anom), deg(sat.M), 1, 2, var+'[deg]','M [deg]',False)

print ('Do you wish to save the graph? (Y/N)')

save = input()

if save == 'Y' or save == 'y':

plotfile(Mvnu_Anom, deg(sat.anom), deg(sat.M), 1, 2, var+'[deg]','M [deg]',True)

print ('\n\nClosing program\n\n')

Here is the introduction video to our presentation. Hope you like it!

Space debree and micrometors post a threat to astronauts onboard the ISS and other spaceships. We can predict impacts, but not where they happen exactly on the outer surface of the ship. To that end, we developed CubeAID. A three phases system that detects, locates and repairs damage caused by microimpacts.

This is how it works. The cubesat orbit allows it to move around the ISS and cover all the possible angles. It takes pictures and sends it to the onboard computer of the ISS and using Watson Image Recognition it locates possible threats to the integrity of the ship.

Once we know the location of the micrometeor impact, the spider robot comes out, analizes the surface and if needed repairs.

Here you can finde our slide presentation!